The sketchbook is an artist’s personal traveling companion, a place to record observations, thoughts, and personal musings and I never leave home without mine. But to find a sketchbook that I actually love to use, is as elusive as it is desirable.
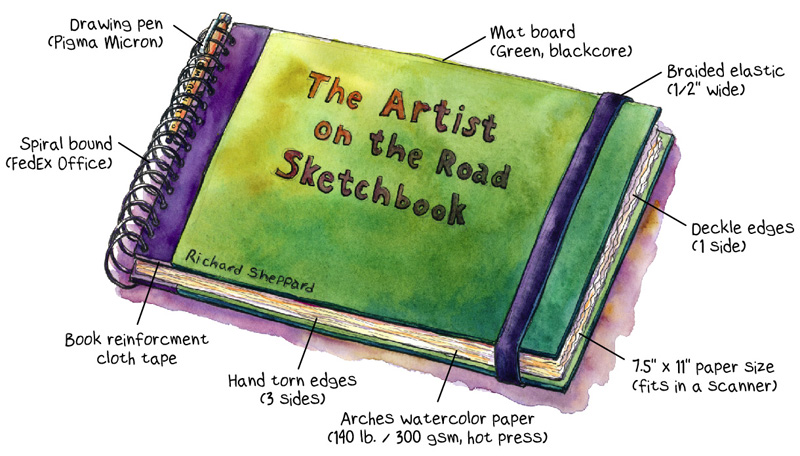
I searched many years for a “just right” sketchbook and a few months ago, after several purchases each proved disappointing, I gave up on commercial brands. Determined to make my own, I bought sheets of Arches hot press paper, linen thread, needles, cloth tape, hole punches, and more. After measuring, marking, stitching, binding, looping, fretting, tearing, and throwing my hands up in the air, I finally landed, what is for me, a near perfect solution.
Its only deficiency is that the binding requires the purchase of a special tool or the help of a third party supplier. Though I tried for weeks to make a stitched binding that worked, it wasn’t until I had the book spiral bound that I found what I was looking for. The spiral binding allows me to tuck the finished pages underneath to save space and to occasionally tear a page out for a friend, sell to a buyer, or toss the occasional, unsightly drawing away. But most important of all, I have my favorite paper to sketch on.
Since making my own sketchbook, I’ve sketched my ramblings around town, hanging out in coffee shops, and roaming the countryside. In fact, I’m so pleased with my sketchbook, I just made two more. So my persistence paid off and now I can concentrate on my true love, sketchbooking.
Excellent solution – and I too love having the paper, size, and format I want. You can even travel with single pages and bind the book at a later date.
Thanks Shirley! I agree, it’s great having the paper, size, and format I want. I’ve used watercolor blocks a quite a while and you are right, I could bind them into a book! Great idea, I just might do that.
This is a great idea… how many full sheets did you use to create this sketchbook? I really like the torn idea. Shirley’s idea of using blog pages would work well too. I don’t like the blocks because I can only work on one page at a time. Often, I like to let one by drying as I tweak another.
Thanks Elizabeth! I used four full sheets and tore them into eight pieces. It’s great because all the deckle edges are on one side. the three other torn sides look great too and give it a real hand-made feel.
Very nice… Brenda Swenson does something similar to make her own sketchbooks… she also adds colored papers too, for a bit of variety. I’m stuck on handbook journals… I love them, and they now make one with heavier paper for watercolor.
Thanks Elaine! I’m not familiar with Brenda Swenson but I’ll look her up. I’m not surprised someone else is doing something similar to this since it works so well. Adding colored paper sounds like a good idea too!
So where/who did the spiral binding?
I do something similar, only I use a product called a Bind-it-All, which uses O-wires rather than a true spiral binding. That allows me to do the whole job myself. The last one I made was a travel journal, and I included text weight papers in between the watercolor papers in order to write notes and my schedule and that sort of thing. It worked well for me.
HI Roger, I had FedEx Office (which use to be Kinko’s) do my binding, but I hear there are a couple of devices that work pretty well that you can buy. The two products I’ve heard of are Zutter’s Bind-It-all and We R Memory Keeper’s The Cinch.
Thanks for the comment Cheryl! I’ve been hearing things about two products: Zutter’s Bind-It-all and We R Memory Keeper’s The Cinch. I think I’m going to have to try one of them out. Have you heard anything in regards to The Cinch? I’m most worried about it not being able to cut through mat board.
I know that the Bind-it-All will punch through mat board – it even punches through book board, which is thicker than mat board. I think the main difference between the two is that the Bind-it-All punches square holes and the Cinch punches round holes.
When I made my travel journal that I mentioned in my last comment, I was meeting a group of artists in New Orleans for an art holiday of sorts, and one of the other participants has both products. She used The Cinch for her journal. I think they’re pretty similar except for the shape of the holes, but since I don’t have The Cinch, I can’t say for sure. I’ve been happy with my Bind-it-All and have no plans to buy The Cinch, but if I were buying today, I would consider The Cinch just for the round holes. Although I don’t mind the square holes either.
After seeing a video about The Cinch, another difference is that you can set which holes actually get punched. I can’t do that with my Bind-it-All. But on the other hand, the smallest diameter wire for The Cinch is 3/4″, while the smallest Bind-it-All wire is 1/2″.
If you buy one, I hope you post about it. I’ll be interested to know which one you decide on.
Thank you Cheryl for all that great information! Sounds like both binders do about an equally good job but there are notable differences like the binding size being larger on the Cinch and the round holes too. I think I’m leaning twords the Cinch because it punches more holes across at once. I might only have to do one punch per page with it.
At the moment I have almost three sketchbooks to fill up so when I get a little farther along with the ones I’ve already made, I’ll probably buy one. and yes, I’ll make sure to post here! Thanks again for your comments!
Classic example of “If you need a job doing well, do it yourself”.
Good guide (and lovely tones & hues as usual). It would be a worthwhile addition to Instructables I think.
Thanks Peter! I tried for many years and bought all kinds of sketchbooks but never found what I was looking for. Good sketchbooks that work for pencil and ink are in abundance but when you get to water media, they all seem to cut corners. The one exception is the watercolor Moleskine. It’s about as good a commercial book as there is but it’s cold press paper not hot press and doesn’t scan as well.
Thanks for the post, I’ve been wanting to use hot press paper in a size that for sketch booking. You demo it in a way that I think I can tackle. I would love to know too, how did you paint the spiral in your sketch? Such small areas, and then to include the pencil!
Thanks Cathy! I hope you try making your very own sketchbook! How did I paint that spiral? He he he. You’ve got a good eye! I tried drawing something that looked good many times but was always disappointed. Then I came up with my final solution. I drew the best spiral circle I could in the front, traced it on a piece of paper, then put the tracing behind my sketchbook page and traced the entire row of spirals. To me if the spiral isn’t perfect, it looks bent and out of shape. Something that is real hard to do. But this technique finally made a drawing I was happy with.
Thanks for the tip! It looks great….love your blog and sketches. They are very inspirational…
Thanks Cathy! You’re very kind.